LeetCode 刷题笔记——day 6

7. 整数反转

难度：简单

给你一个 32 位的有符号整数 x ，返回将 x 中的数字部分反转后的结果。

如果反转后整数超过 32 位的有符号整数的范围 [−231, 231 − 1] ，就返回 0。

假设环境不允许存储 64 位整数（有符号或无符号）。

示例 1：

1
2
输入：x = 123
输出：321

示例 2：

1
2
输入：x = -123
输出：-321

示例 3：

1
2
输入：x = 120
输出：21

示例 4：

1
2
输入：x = 0
输出：0

提示：

  • -231 <= x <= 231 - 1

我的答案

思路

先取 x 的绝对值，创建一个较大的 long 类型变量 n，从 x 的个位开始遍历每一位数字并依次赋给 n，此外还要考虑每个整数的范围问题。看完题解才注意到题目：假设环境不允许存储 64 位整数（有符号或无符号）。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
class Solution {
public:
    int reverse(int x) {
        bool notion = true;
        long x0 = x;
        if(x0 < 0) {
            x0 = -x0;
            notion = !notion;
        }

        long n = 0;
        for(int i = 1; x0 > 0; i++) {
            n *= 10;
            n += x0 % 10;
            x0 /= 10;
        }
        n = notion ? n : -n;

        if(n > INT_MAX || n < INT_MIN) return 0;

        return n;
    }
};

  • 执行用时: 0 ms

  • 内存消耗: 5.8 MB

一直考虑不全面，考虑了 n 的范围，却很容易忽略 x 取绝对值后的范围，而且审题不清楚，导致方法从一开始就是错的，虽然可以通过力扣的测试用例。

官方答案

数学

思路

记rev\textit{rev} 为翻转后的数字，为完成翻转，我们可以重复「弹出」xx 的末尾数字，将其「推入」rev\textit{rev} 的末尾，直至xx 为00。

要在没有辅助栈或数组的帮助下「弹出」和「推入」数字，我们可以使用如下数学方法：

1
2
3
4
5
6
// 弹出 x 的末尾数字 digit
digit = x % 10
x /= 10

// 将数字 digit 推入 rev 末尾
rev = rev * 10 + digit

题目需要判断反转后的数字是否超过3232 位有符号整数的范围[−231,231−1][-2^{31},2^{31}-1]，例如x=2123456789x=2123456789 反转后的rev=9876543212>231−1=2147483647\textit{rev}=9876543212>2^{31}-1=2147483647，超过了3232 位有符号整数的范围。

因此我们需要在「推入」数字之前，判断是否满足

−231≤rev⋅10+digit≤231−1-2^{31}\le\textit{rev}\cdot10+\textit{digit}\le2^{31}-1

若该不等式不成立则返回00。

但是题目要求不允许使用6464 位整数，即运算过程中的数字必须在3232 位有符号整数的范围内，因此我们不能直接按照上述式子计算，需要另寻他路。

考虑x>0x>0 的情况，记INT_MAX=231−1=2147483647\textit{INT\_MAX}=2^{31}-1=2147483647，由于

则不等式

rev⋅10+digit≤INT_MAX\textit{rev}\cdot10+\textit{digit}\le\textit{INT\_MAX}

等价于

rev⋅10+digit≤⌊INT_MAX10⌋⋅10+7\textit{rev}\cdot10+\textit{digit}\le\lfloor\dfrac{\textit{INT\_MAX}}{10}\rfloor\cdot10+7

移项得

(rev−⌊INT_MAX10⌋)⋅10≤7−digit(\textit{rev}-\lfloor\dfrac{\textit{INT\_MAX}}{10}\rfloor)\cdot10\le7-\textit{digit}

讨论该不等式成立的条件：

若rev>⌊INT_MAX10⌋\textit{rev}>\lfloor\cfrac{\textit{INT\_MAX}}{10}\rfloor，由于digit≥0\textit{digit}\ge0，不等式不成立。
若rev=⌊INT_MAX10⌋\textit{rev}=\lfloor\cfrac{\textit{INT\_MAX}}{10}\rfloor，当且仅当digit≤7\textit{digit}\le7 时，不等式成立。
若rev<⌊INT_MAX10⌋\textit{rev}<\lfloor\cfrac{\textit{INT\_MAX}}{10}\rfloor，由于digit≤9\textit{digit}\le9，不等式成立。

注意到当rev=⌊INT_MAX10⌋\textit{rev}=\lfloor\cfrac{\textit{INT\_MAX}}{10}\rfloor 时若还能推入数字，则说明xx 的位数与INT_MAX\textit{INT\_MAX} 的位数相同，且要推入的数字digit\textit{digit} 为xx 的最高位。由于xx 不超过INT_MAX\textit{INT\_MAX}，因此digit\textit{digit} 不会超过INT_MAX\textit{INT\_MAX} 的最高位，即digit≤2\textit{digit}\le2。所以实际上当rev=⌊INT_MAX10⌋\textit{rev}=\lfloor\cfrac{\textit{INT\_MAX}}{10}\rfloor 时不等式必定成立。

因此判定条件可简化为：当且仅当rev≤⌊INT_MAX10⌋\textit{rev}\le\lfloor\cfrac{\textit{INT\_MAX}}{10}\rfloor 时，不等式成立。

x<0x<0 的情况类似，留给读者自证，此处不再赘述。

综上所述，判断不等式

−231≤rev⋅10+digit≤231−1-2^{31}\le\textit{rev}\cdot10+\textit{digit}\le2^{31}-1

是否成立，可改为判断不等式

⌈−23110⌉≤rev≤⌊231−110⌋\lceil\cfrac{-2^{31}}{10}\rceil\le\textit{rev}\le\lfloor\dfrac{2^{31}-1}{10}\rfloor

是否成立，若不成立则返回00。

作者：LeetCode-Solution

妙妙妙 ~ 这样分析下来，就用很少的代码解决了问题。

现在用 C++ 实现一遍：

1
2
3
4
5
6
7
8
9
10
11
12
class Solution {
public:
    int reverse(int x) {
        int n = 0;
        while(x != 0) {
            if(n < INT_MIN / 10 || n > INT_MAX / 10) return 0;
            n = n * 10 + x % 10;
            x /= 10;
        }
        return n;
    }
};

  • 执行用时: 0 ms

  • 内存消耗: 5.8 MB

同样练习一下 Java 来实现：

1
2
3
4
5
6
7
8
9
10
11
class Solution {
    public int reverse(int x) {
        int n = 0;
        while(x != 0) {
            if(n < Integer.MIN_VALUE / 10 || n > Integer.MAX_VALUE / 10) return 0;
            n = n * 10 + x % 10;
            x /= 10;
        }
        return n;
    }
}

  • 执行用时: 0 ms

  • 内存消耗: 35.7 MB

8. 字符串转换整数 (atoi)

难度：中等

请你来实现一个 myAtoi(string s) 函数，使其能将字符串转换成一个 32 位有符号整数（类似 C/C++ 中的 atoi 函数）。

函数 myAtoi(string s) 的算法如下：

  • 读入字符串并丢弃无用的前导空格
  • 检查下一个字符（假设还未到字符末尾）为正还是负号，读取该字符（如果有）。 确定最终结果是负数还是正数。 如果两者都不存在，则假定结果为正。
  • 读入下一个字符，直到到达下一个非数字字符或到达输入的结尾。字符串的其余部分将被忽略。
  • 将前面步骤读入的这些数字转换为整数（即，“123” -> 123， “0032” -> 32）。如果没有读入数字，则整数为 0 。必要时更改符号（从步骤 2 开始）。
  • 如果整数数超过 32 位有符号整数范围 [−231, 231 − 1] ，需要截断这个整数，使其保持在这个范围内。具体来说，小于 −231 的整数应该被固定为 −231 ，大于 231 − 1 的整数应该被固定为 231 − 1 。
  • 返回整数作为最终结果。

注意：

  • 本题中的空白字符只包括空格字符 ' ' 。
  • 除前导空格或数字后的其余字符串外，请勿忽略 任何其他字符。

示例 1：

1
2
3
4
5
6
7
8
9
10
11
输入：s = "42"
输出：42
解释：加粗的字符串为已经读入的字符，插入符号是当前读取的字符。
第 1 步："42"（当前没有读入字符，因为没有前导空格）
         ^
第 2 步："42"（当前没有读入字符，因为这里不存在 '-' 或者 '+'）
         ^
第 3 步："42"（读入 "42"）
           ^
解析得到整数 42 。
由于 "42" 在范围 [-231, 231 - 1] 内，最终结果为 42 。

示例 2：

1
2
3
4
5
6
7
8
9
10
11
输入：s = "   -42"
输出：-42
解释：
第 1 步："   -42"（读入前导空格，但忽视掉）
            ^
第 2 步："   -42"（读入 '-' 字符，所以结果应该是负数）
             ^
第 3 步："   -42"（读入 "42"）
               ^
解析得到整数 -42 。
由于 "-42" 在范围 [-231, 231 - 1] 内，最终结果为 -42 。

示例 3：

1
2
3
4
5
6
7
8
9
10
11
输入：s = "4193 with words"
输出：4193
解释：
第 1 步："4193 with words"（当前没有读入字符，因为没有前导空格）
         ^
第 2 步："4193 with words"（当前没有读入字符，因为这里不存在 '-' 或者 '+'）
         ^
第 3 步："4193 with words"（读入 "4193"；由于下一个字符不是一个数字，所以读入停止）
             ^
解析得到整数 4193 。
由于 "4193" 在范围 [-231, 231 - 1] 内，最终结果为 4193 。

示例 4：

1
2
3
4
5
6
7
8
9
10
11
输入：s = "words and 987"
输出：0
解释：
第 1 步："words and 987"（当前没有读入字符，因为没有前导空格）
         ^
第 2 步："words and 987"（当前没有读入字符，因为这里不存在 '-' 或者 '+'）
         ^
第 3 步："words and 987"（由于当前字符 'w' 不是一个数字，所以读入停止）
         ^
解析得到整数 0 ，因为没有读入任何数字。
由于 0 在范围 [-231, 231 - 1] 内，最终结果为 0 。

示例 5：

1
2
3
4
5
6
7
8
9
10
11
输入：s = "-91283472332"
输出：-2147483648
解释：
第 1 步："-91283472332"（当前没有读入字符，因为没有前导空格）
         ^
第 2 步："-91283472332"（读入 '-' 字符，所以结果应该是负数）
          ^
第 3 步："-91283472332"（读入 "91283472332"）
                     ^
解析得到整数 -91283472332 。
由于 -91283472332 小于范围 [-231, 231 - 1] 的下界，最终结果被截断为 -231 = -2147483648 。

提示：

  • 0 <= s.length <= 200
  • s 由英文字母（大写和小写）、数字（0-9）、' '、'+'、'-' 和 '.' 组成

我的答案

思路

根据题目要求的步骤，先把无用的前导空格丢弃，剩下的所有字符先放进字符数组 ch 中，然后依次读取字符，只取第一串数字，同时注意正负号及整数范围的影响。这里全部当作正数，最后统一判断输出，简化中间计算。特别是负数的范围，由于负数比整数多一位，所以直接对 INT_MIN 取正会导致超出，这里使用 num - 1 > -(INT_MIN+1) 控制负数的范围。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
class Solution {
public:
    int myAtoi(string s) {
        vector<char> ch(s.size() + 1);
        int j = 0, l = 0;
        long num = 0;
        for(int i = 0; i < s.size(); i++) {
            if(s[i] != ' ' || l) {
                ch[j++] = s[i];
                l = 1;
            }
        }
        ch[j] = '\0';

        int m = 1;
        if(ch[0] == '-') {
            m = 0;
        } else if(ch[0] == '+') m = 2;

        for(int i = 0; ch[i] != '\0'; i++) {
            if((m == 0 || m == 2) && i == 0) continue;
            if(ch[i] <= '9' && ch[i] >= '0') {
                num = num * 10 + (int)(ch[i] - '0');
                if(m && num > INT_MAX) return INT_MAX;
                if(!m && num - 1 > -(INT_MIN+1)) return INT_MIN;
            } else break;
        }

        return m ? num : -num;
    }
};

  • 执行用时: 8 ms

  • 内存消耗: 7 MB

官方答案

在官方题解中，又为我们引出了新的方法：

自动机

思路

字符串处理的题目往往涉及复杂的流程以及条件情况，如果直接上手写程序，一不小心就会写出极其臃肿的代码。

因此，为了有条理地分析每个输入字符的处理方法，我们可以使用自动机这个概念：

我们的程序在每个时刻有一个状态 s，每次从序列中输入一个字符 c，并根据字符 c 转移到下一个状态 s’。这样，我们只需要建立一个覆盖所有情况的从 s 与 c 映射到 s’ 的表格即可解决题目中的问题。

算法

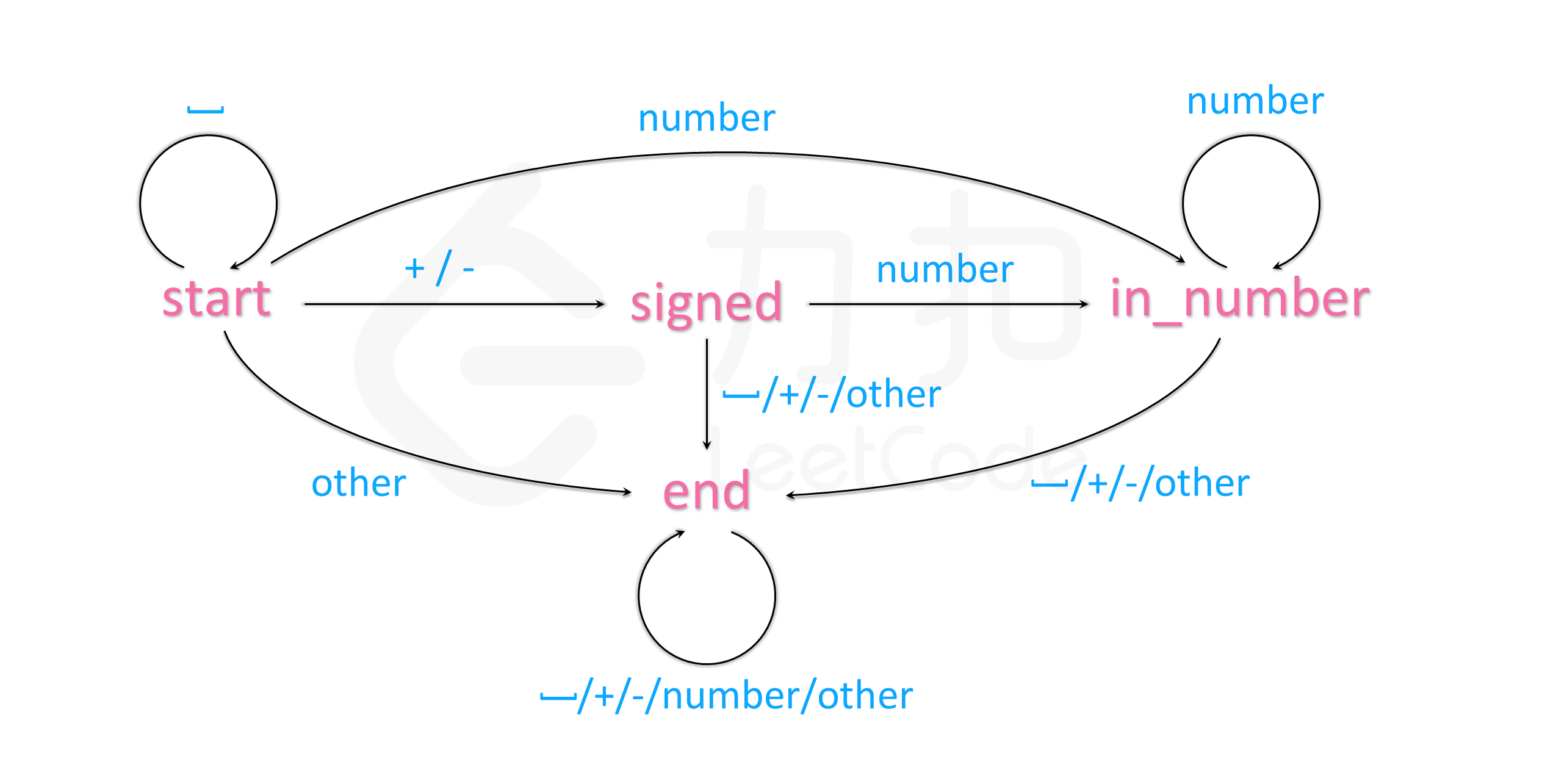
本题可以建立如下图所示的自动机：

自动机图示

我们也可以用下面的表格来表示这个自动机：

’ ’+/-numberother
startstartsignedin_numberend
signedendendin_numberend
in_numberendendin_numberend
endendendendend

接下来编程部分就非常简单了：我们只需要把上面这个状态转换表抄进代码即可。

另外自动机也需要记录当前已经输入的数字，只要在 s' 为 in_number 时，更新我们输入的数字，即可最终得到输入的数字。

作者：LeetCode-Solution

这里用 C++ 复现了一遍：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
class AutoMaton {
    string state = "start";
    unordered_map<string, vector<string>> table = {
        {"start", {"start", "signed", "digit", "end"}},
        {"signed", {"end", "end", "digit", "end"}},
        {"digit", {"end", "end", "digit", "end"}},
        {"end", {"end", "end", "end", "end"}}
    };
    int getCol(char c) {
        if(isspace(c)) return 0;
        if(c == '+' || c == '-') return 1;
        if(isdigit(c)) return 2;
        return 3;
    }

public:
    int sign = 1;
    long ans = 0;
    void get(char c) {
        state = table[state][getCol(c)];
        if(state == "digit") {
            ans = ans * 10 + c - '0';
            ans = sign == 1 ? min(ans, (long)INT_MAX) : min(ans, -(long)INT_MIN);
        } else if(state == "signed") sign = c == '+' ? 1 : -1;
    }
};
class Solution {
public:
    int myAtoi(string s) {
        AutoMaton am;
        for(char c : s) am.get(c);
        return am.sign * am.ans;
    }
};

  • 执行用时: 16 ms

  • 内存消耗: 10.5 MB

学到了学到了，这种方法确实感觉非常不赖，不过代码量还是挺大的。这里还涉及到一个小知识点：

C++ 中的 min() 函数接收两个相同类型的参数并返回较小值

注意，是相同类型的参数。在我编辑代码的时候就因为给 min() 的参数为 long 类型的 ans 和 int 类型的 INT_MAX ，虽然都是整数，但确实是不同的类型，这里使用 (long) 对 INT_MAX 做了强制类型转换。

老规矩，再练习一遍用 Java 来实现：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
class Solution {
    public int myAtoi(String s) {
        AutoMoton am = new AutoMoton();
        int len = s.length();
        for(int i = 0; i < len; i++) {
            am.get(s.charAt(i));
        }
        return (int)am.ans * am.sign;
    }
}

class AutoMoton {
    public int sign = 1;
    public long ans = 0;
    private String state = "start";
    private Map<String, String[]> table = new HashMap<String, String[]>() {{
        put("start", new String[]{"start", "signed", "digit", "end"});
        put("signed", new String[]{"end", "end", "digit", "end"});
        put("digit", new String[]{"end", "end", "digit", "end"});
        put("end", new String[]{"end", "end", "end", "end"});
    }};

    private int getCol(char c) {
        if(c == ' ') return 0;
        if(c == '+' || c == '-') return 1;
        if(Character.isDigit(c)) return 2;
        return 3;
    }

    public void get(char c) {
        state = table.get(state)[getCol(c)];
        if(state.equals("digit")) {
            ans = ans * 10 + c - '0';
            ans = sign == 1 ? Math.min(ans, (long)Integer.MAX_VALUE) : Math.min(ans, -(long)Integer.MIN_VALUE);
        } else if(state.equals("signed")) sign = c == '+' ? 1 : -1;
    }
}

  • 执行用时: 3 ms

  • 内存消耗: 38.4 MB

总结

今天做题速度依然非常慢，效率还是低了一点。