算法——union-find

前言
零基础直接刷力扣还是有些虎了，所以特意补一下理论知识。本系列笔记将以图灵社区出版的《算法：第4版》为主要参考复现各种算法及实现过程，试图以自己的方式深度解析算法。

需求

一列已知的步长为 1 且从 0 开始依次递增的整数序列，对于成对整数 p 和 q ，即认为 p 与 q 相连。“相连”是一种等价关系，即具有自反性p 和 p 是相连的。、对称性如果 p 和 q 是相连的，那么 q 和 p 也是相连的。与传递性如果 p 和 q 是相连的且 q 和 r 是相连的，那么 p 和 r 也是相连的。。现程序从输入中读取一对整数 p 和 q ，假设 p 和 q 都存在于已知序列中，若序列中对应整数相连，则不做操作，若序列中对应整数不相连，则将他们相连，并将 p 和 q 输出。

思路

主要问题在于，我们需要判断输入的一对整数在已知序列中是否相连，这意味着我们需要标记哪些整数对相连，并且由于输入的整数对能够创建新的连接，因此我们需要在每次输入时维护这些标记。

等价关系的传递性决定了序列中所有的整数都可以分为几个块，或称连通分量，在一个块内的所有整数都在两两相连的同时不具有任何对外的连接，而为分属两个连通分量的整数创建连接时则会合并这两个块。注意初始时每个块都只有一个元素。

一个中规模连通性问题的图示，图源自《算法：第4版》

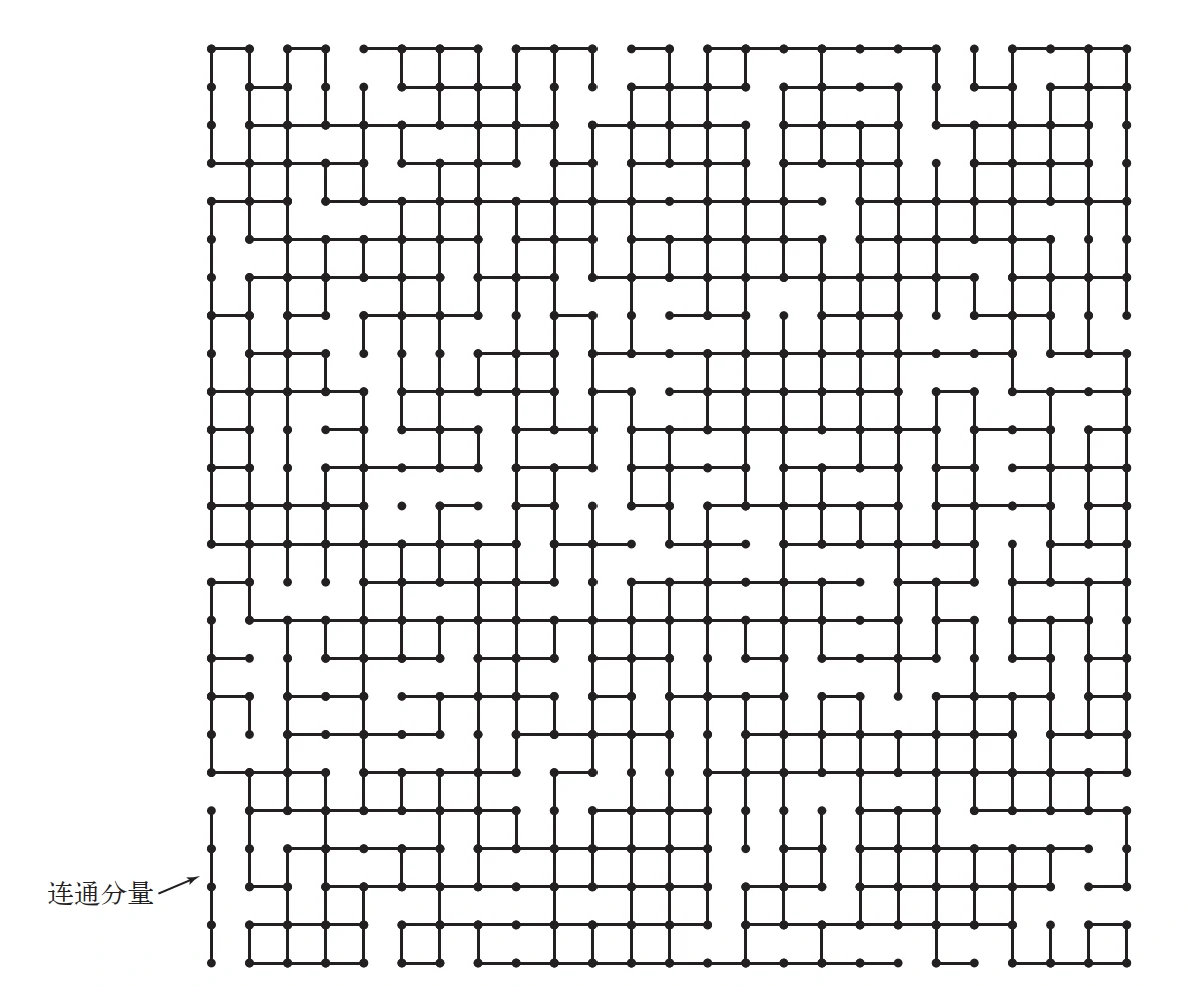
因此，我们实际上只需要标记每个整数属于哪个块就行了，在输入后判断两个整数是否相连，若不相连则将两个整数分属的两个块的所有元素都设置为同一标记以将他们相连。

API 设计

首先我们需要初始化序列，即将每个整数标识为他们所属的块，而初始时每个元素都各属于一个块。然后对输入的整数对进行判断，需设置一个判断整数对是否相连的方法，若整数对不相连，我们则使用一个将他们相连的方法。而在判断相连的方法中，实际上就是比较该整数对所属块的标识，如果设置一个返回标识的函数，可以进一步简化操作。

因此，提供如下四个 API 即可：

API	备注
void union_find(int N)	初始化
void union(int p, int q)	连接 p, q
int find(int p)	返回标识
boolean connected(int p, int q)	判断 p, q 是否相连

基础实现

我们使用 union_find 类封装该算法，数据的输入及测试交由类中的静态 main() 方法完成。实现算法除以上 API 外还需要一个数组用于初始化及标识序列，数组以序列中的整数为索引，对应值为整数所属块的标识，声明如下：

1	private int[] id;

初始化方法
由于序列步长为 1 且从 0 开始递增，我们只需给定序列长度即可，因此初始序列由一个整数 N 决定。对每个整数的初始标识，让其等于整数本身即可。此外因为 union_find 类的实现必须基于初始序列，因此我们将初始化方法 uinon_find() 定义为不可选的构造方法。
实现如下：
1
2
3
4
public union_find(int N) {
id = new int[N];
for (int i = 0; i < N; i++) id[i] = i;
}
判断方法
判断方法 connected() 返回判断两个整数的标识是否相同的布尔值即可，在我们设计 API 的时候，整数的标识可以由 find() 方法返回，因此 connected() 方法只需判断 find() 方法的返回值即可。
实现如下：
1
2
3
public boolean connected(int p, int q) {
return find(p) == find(q);
}

测试方法

返回标识及连接方法复杂一些，我们作为关键方法，先实现最终的测试方法 main() 。main() 首先需要输入一个整数，即初始序列长度由我们给定。然后在输入中依次读取整数对并依靠我们给定的 API 进行具体操作：首先调用 connected() 方法判断输入的整数对是否已经相连，若相连则忽略，若不相连则调用 union() 方法来连接并在屏幕上输出这对整数。此外，为方便测试，输入采用文件形式，而非控制台输入模式，注意需抛出异常 FileNotFoundException。

实现如下：

public static void main(String[] args) throws FileNotFoundException {
    Scanner sc = new Scanner(new FileReader("demo.txt"));
    int N = sc.nextInt();
    union_find uf = new union_find(N);
    while (sc.hasNext()) {
        int p = sc.nextInt();
        int q = sc.nextInt();
        if (uf.connected(p, q)) continue;
        uf.union(p, q);
        System.out.println(p + ' ' + q);
    }
    sc.close();
}

基础封装

基于以上实现我们便搭建好了算法的基础框架，因此该算法的基础实现如下：

import java.io.FileNotFoundException;
import java.io.FileReader;
import java.util.Scanner;

public class union_find {
    private int[] id;
    public union_find(int N) {
        id = new int[N];
        for (int i = 0; i < N; i++) id[i] = i;
    }
    public boolean connected(int p, int q) {
        return find(p) == find(q);
    }
    public int find(int p) {return 0;}
    public void union(int p, int q) {}
    public static void main(String[] args) throws FileNotFoundException {
        Scanner sc = new Scanner(new FileReader("demo.txt"));
        int N = sc.nextInt();
        union_find uf = new union_find(N);
        while (sc.hasNext()) {
            int p = sc.nextInt();
            int q = sc.nextInt();
            if (uf.connected(p, q)) continue;
            uf.union(p, q);
            System.out.println(p + " " + q);
        }
        sc.close();
    }
}

关键实现

在 union-find 算法中，关键方法就是 find() 与 union() 方法了。find() 方法负责查找并返回整数所在块的标识， union() 方法负责连接两个不相连的整数。如何实现这两个方法取决于我们如何标识特定的块，在基础实现中我们将标识存储在数组中，并以整数值作索引。

quick-find 算法

一种简单的思路是将属于同一块的整数对应的标识符设为相同，这就意味着当我们创建新的连接的时候，需要将两个整数分属的两个块的所有整数的标识设为相同。基于这个思路，find() 方法只需要返回以当前整数为索引的对应数组元素即可：

1	public int find(int p) {return id[p];}

而连接和维护标识的操作则全部交给了 union() 方法。我们称这个算法为 quick-find 算法。

union() 方法接收两位整数并将他们分属的两个块中的整数的标识全部设为相同值，除了标识相同，相同块中的元素并没有任何特征，因此我们需要遍历整个数组找到相应标识的元素并修改他们。可以以其中一个块原有的标识作为新标识，这样，我们就不需要修改两个块所有元素的标识，同时不用担心与其他块的标识重复而导致的逻辑错误。这里我们统一使用传入整数对 p 、 q 中 q 的标识作为新标识，实现如下：

public void union(int p, int q) {
	int qID = find(q);
	int pID = find(p);
	for (int i = 0; i < id.length; i++) 
		if(id[i] == pID) id[i] = qID;
}

因此， quick-find 算法的实现就完成了：

import java.io.FileNotFoundException;
import java.io.FileReader;
import java.util.Scanner;

public class union_find {
    private int[] id;
    public union_find(int N) {
        id = new int[N];
        for (int i = 0; i < N; i++) id[i] = i;
    }
    public boolean connected(int p, int q) {
        return find(p) == find(q);
    }
    public int find(int p) {return id[p];}
    public void union(int p, int q) {
        int qID = find(q);
        int pID = find(p);
        for (int i = 0; i < id.length; i++)
            if(id[i] == pID) id[i] = qID;
    }
    public static void main(String[] args) throws FileNotFoundException {
        Scanner sc = new Scanner(new FileReader("demo.txt"));
        int N = sc.nextInt();
        union_find uf = new union_find(N);
        while (sc.hasNext()) {
            int p = sc.nextInt();
            int q = sc.nextInt();
            if (uf.connected(p, q)) continue;
            uf.union(p, q);
            System.out.println(p + " " + q);
        }
        sc.close();
    }
}

quick-union 算法

虽然说 quick-find 算法十分简洁，但是由于每一次输入都需要遍历整个数组，一般无法用于处理大型问题，因此我们需要一些别的思路：如果是仅仅把同块元素的标识设为相同，则对于同块元素的查找就必须遍历数组才行，因此我们的重点应该是把同块元素在逻辑上连接在一起，这样查找同块元素就不需要涉及对数组其他元素的访问了。

我们可以以一个块中最早的整数为根整数，而其他整数直接或间接地指向这个根整数，所谓直接或间接指向，即同块中的一个整数索引到的数组值可以是这个根整数，也可以是其他能够指向根整数的整数值。而根整数索引到的值始终与初始状态相同，即块中根整数的标识为其本身。举个例子，当我们要查找一个整数 p 所属块的标识的时候，我们需要查询以 p 为索引在数组中对应的值 id[p] ，然后再以 id[p] 为索引得到 id[id[p]] ……一直到某个索引值与存储值相同id[x] == x时，该值即为该块的标识，也就是该块中根整数的值。而连接两个块时只需将一个块中根整数索引到数组中的值换成另一个块的根整数即可。

这么解释或许过于抽象，下图为《算法：第4版》中的图示，根触点即所谓根整数。

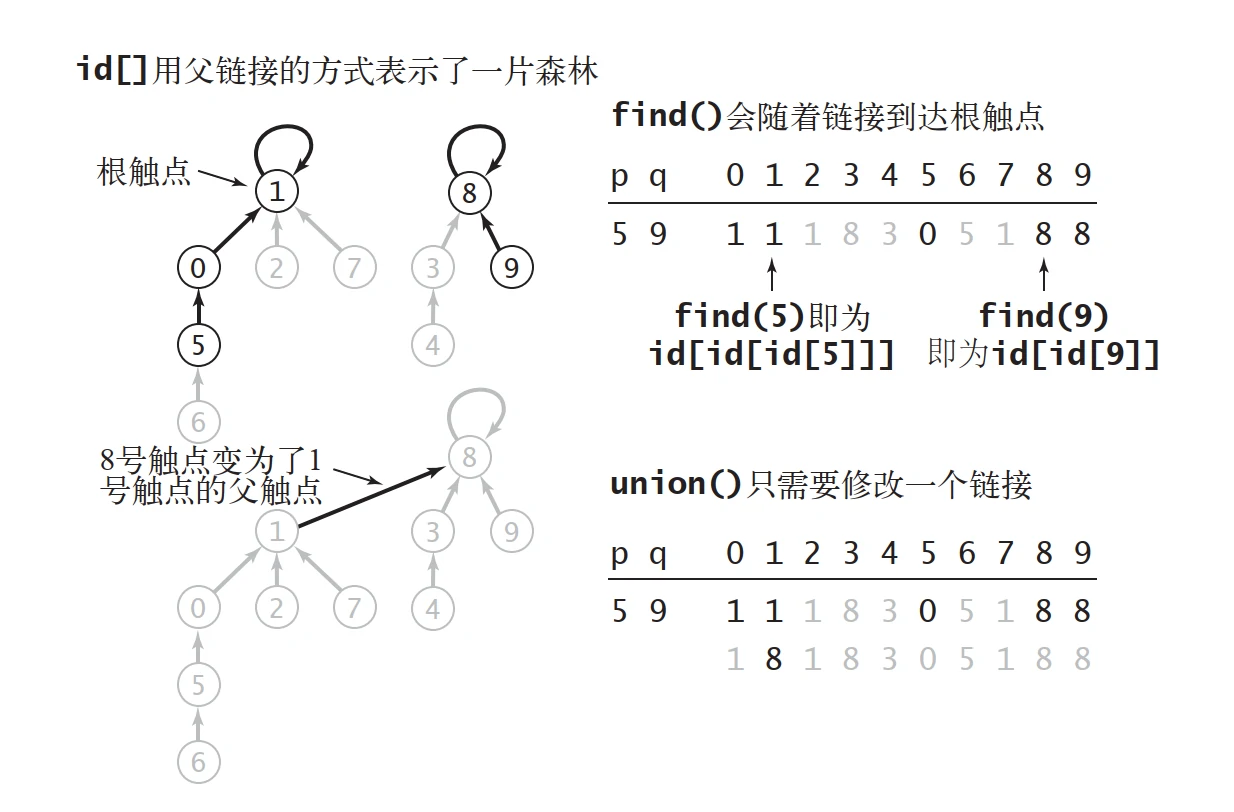quick-union 算法概述，图源自《算法：第4版》

这个思路貌似让 find() 方法变得非常复杂，事实上实现并不复杂。我们只需要根据根整数索引到的值等于本身，而同块中其他整数索引到的值都不等于本身的特性来实现一个 while 循环，当索引等于数组中的存储值时，该值即该块的标识。

实现如下：

public int find(int p) {
	while (p != id[p]) p = id[p];
	return p;
}

另一方面，union() 方法的任务就非常简单了，不仅不用遍历数组，而且只需修改一个值即可。也就是为什么算法名为 quick-union 算法了。这里对于任何输入整数对 p 、 q ，总是以 q 的根整数为新的根整数：

public void union(int p, int q) {
	int pRoot = find(p);
	int qRoot = find(q);
	id[pRoot] = qRoot;
}

这样，我们就实现了更快一点的 quick-union 算法了：

import java.io.FileNotFoundException;
import java.io.FileReader;
import java.util.Scanner;

public class union_find {
    private int[] id;
    public union_find(int N) {
        id = new int[N];
        for (int i = 0; i < N; i++) id[i] = i;
    }
    public boolean connected(int p, int q) {
        return find(p) == find(q);
    }
    public int find(int p) {
        while (p != id[p]) p = id[p];
        return p;
    }
    public void union(int p, int q) {
        int pRoot = find(p);
        int qRoot = find(q);
        id[pRoot] = qRoot;
    }
    public static void main(String[] args) throws FileNotFoundException {
        Scanner sc = new Scanner(new FileReader("demo.txt"));
        int N = sc.nextInt();
        union_find uf = new union_find(N);
        while (sc.hasNext()) {
            int p = sc.nextInt();
            int q = sc.nextInt();
            if (uf.connected(p, q)) continue;
            uf.union(p, q);
            System.out.println(p + " " + q);
        }
        sc.close();
    }
}

加权 quick-union 算法

上面的 quick-union 算法虽说已经相较于 quick-find 算法提示不少了，但是在最终实现时，显然还有一个不太高效的假设：对于任何输入整数对 p 、 q ，总是以 q 的根整数为新的根整数。

由于我们总是无条件将 q 所在块通过原根整数间接接入新块，如果将一个块的连接关系描述成一棵连接树的话，这将导致树的高度不断提高，也就增加了 find() 方法中循环的次数，如图所示：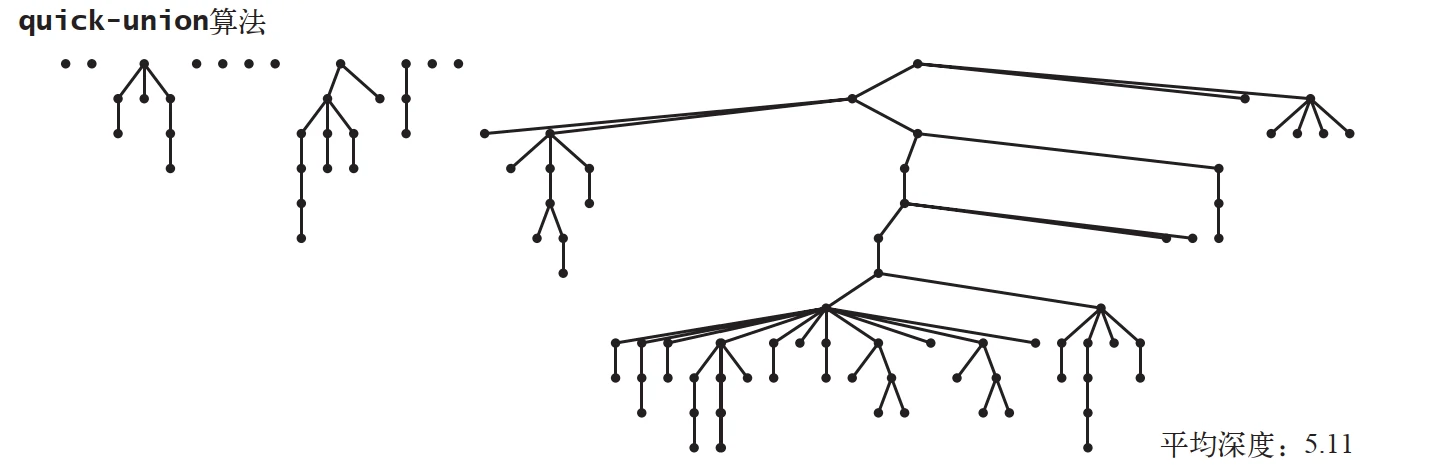

quick-union 生成的树，图源自《算法：第4版》

先思考一个问题，为什么上述的树会不断长高。当我们连接两棵树的时候，两棵树如果本来就有高度的区别，那么将小树连接到一棵大树上的时候，树的高度并不会有什么变化，而当将一棵大树连接到一棵小树上时，由于根整数将指向小树的根整数，因此新树的高度将加一，而问题则显然出在这里。想象一下，如果运气不好，每次都将大树连接到小树，则最后生成的树的高度可能会等于初始序列的长度，这意味着每次调用 find() 方法将遍历整个数组，毫无性能可言！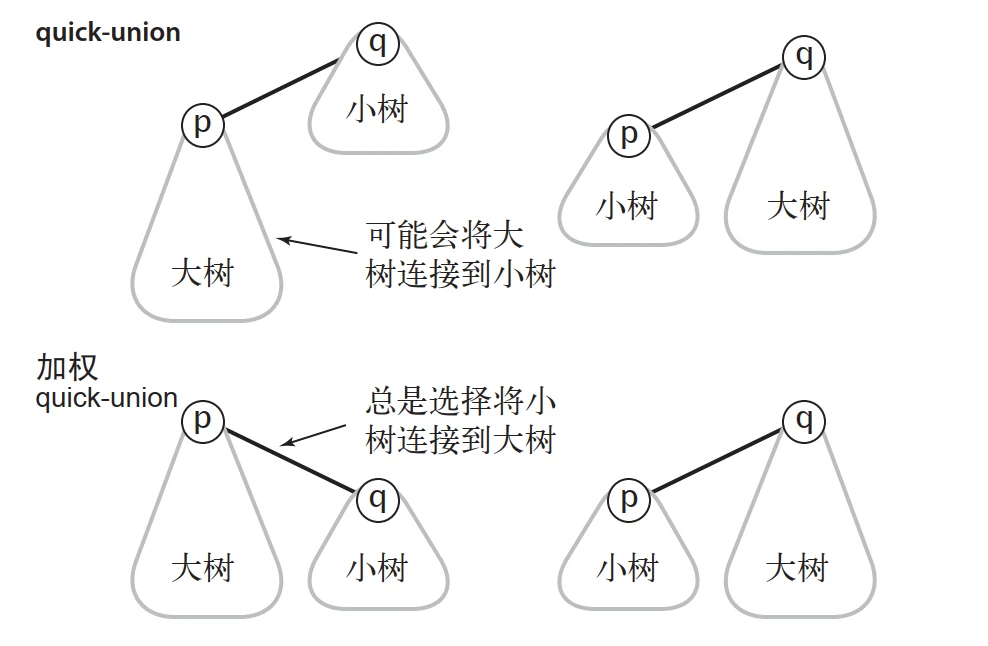

加权 quick-union，图源自《算法：第4版》

如果我们每次连接两棵树的时候，依据树的大小关系，总是把较小的树接入较大的树，就能很大程度解决这个问题了。因此，我们最后一步将对这个问题进行优化，所采用的方法就是加权。

由于 quick-union 算法树与树之间实际上就是根整数与根整数之间的操作，因此我们只需为每棵树的根整数加权并在每次连接前进行比较即可。根据上文的分析，权值大小应与树的高度有关，但事实上树的高度的维护会复杂一些。其实我们可以直接依据树中整数的个数，即节点数来作为权值，毕竟，当总是小树接入大树的话，从一开始就不会生成节点少而高度大的怪树，而维护一个用节点数表示的权值也比维护一个高度表示的要容易。

我们额外定义一个数组，数组中的值表示对应整数作为根整数的时候所拥有的节点数，初始状态每个元素自成一组，一组一个元素，因此初始化时将数组中的值全部设为 1 即可。

实现如下：

private int[] sz;
public union_find(int N) {
	id = new int[N];
    sz = new int[N];
	for (int i = 0; i < N; i++) {
        id[i] = i;
        sz[i] = 1;
    }
}

然后修改一下 union() 方法的实现，在连接树之前先进行比较，连接后将总节点数存储在新根整数索引到的数组位里。

实现如下：

public void union(int p, int q) {
    int pRoot = find(p);
    int qRoot = find(q);
    if (sz[pRoot] < sz[qRoot]) {
    	id[pRoot] = qRoot;
    	sz[qRoot] += sz[pRoot];
    } else {
    	id[qRoot] = pRoot;
    	sz[pRoot] += sz[qRoot];
    }
}

这样，我们就实现了加权 quick-union 算法：

import java.io.FileNotFoundException;
import java.io.FileReader;
import java.util.Scanner;

public class union_find {
    private int[] id;
    private int[] sz;
    public union_find(int N) {
        id = new int[N];
        sz = new int[N];
        for (int i = 0; i < N; i++) {
            id[i] = i;
            sz[i] = 1;
        }
    }
    public boolean connected(int p, int q) {
        return find(p) == find(q);
    }
    public int find(int p) {
        while (p != id[p]) p = id[p];
        return p;
    }
    public void union(int p, int q) {
        int pRoot = find(p);
        int qRoot = find(q);
        if (sz[pRoot] < sz[qRoot]) {
            id[pRoot] = qRoot;
            sz[qRoot] += sz[pRoot];
        } else {
            id[qRoot] = pRoot;
            sz[pRoot] += sz[qRoot];
        }
    }
    public static void main(String[] args) throws FileNotFoundException {
        Scanner sc = new Scanner(new FileReader("demo.txt"));
        int N = sc.nextInt();
        union_find uf = new union_find(N);
        while (sc.hasNext()) {
            int p = sc.nextInt();
            int q = sc.nextInt();
            if (uf.connected(p, q)) continue;
            uf.union(p, q);
            System.out.println(p + " " + q);
        }
        sc.close();
    }
}

该算法效果如图所示：

加权 quick-union，图源自《算法：第4版》

当然，如果以高度作为权值的话，实现就应该是下面这样：

public void union(int p, int q) {
    int pRoot = find(p);
    int qRoot = find(q);
    if (sz[pRoot] < sz[qRoot]) id[pRoot] = qRoot;
    else if (sz[pRoot] > sz[qRoot]) id[qRoot] = pRoot;
    else {
        id[pRoot] = qRoot;
        sz[qRoot]++;
    }
}

路径压缩的加权 quick-union 算法
即使加权 quick-union 算法，依然不是现存的最优算法，即使树的高度得到了很大的控制，但我们依然希望每个节点能直接连接到根整数。
路径压缩的加权 quick-union 算法是最优的算法，但并非所有操作都能在常数时间内完成。
摘自：《算法：第4版》。
该算法的实现实际上就是在 find() 方法中添加一个循环，把查找过程中遇到的中间节点全部改为指向根整数的，以最大化压缩路径，得到一棵几乎扁平的树。
实现如下：
1
2
3
4
5
6
7
8
9
10
public int find(int p) {
int tmp = p;
while (p != id[p]) p = id[p];
while (tmp != id[tmp]) {
int t = tmp;
tmp = id[tmp];
id[t] = p;
}
return p;
}
该算法的具体实现及其他语言实现将在下面给出。

源代码

import java.io.FileNotFoundException;
import java.io.FileReader;
import java.util.Scanner;

public class union_find {
    private int[] id;
    private int[] sz;
    public union_find(int N) {
        id = new int[N];
        sz = new int[N];
        for (int i = 0; i < N; i++) {
            id[i] = i;
            sz[i] = 1;
        }
    }
    public boolean connected(int p, int q) {
        return find(p) == find(q);
    }
    public int find(int p) {
        int tmp = p;
        while (p != id[p]) p = id[p];
        while (tmp != id[tmp]) {
            int t = tmp;
            tmp = id[tmp];
            id[t] = p;
        }
        return p;
    }
    public void union(int p, int q) {
        int pRoot = find(p);
        int qRoot = find(q);
        if (pRoot == qRoot)
            return;
        if (sz[pRoot] < sz[qRoot]) {
            id[pRoot] = qRoot;
            sz[qRoot] += sz[pRoot];
        } else {
            id[qRoot] = pRoot;
            sz[pRoot] += sz[pRoot];
        }
    }
    public static void main(String[] args) throws FileNotFoundException {
        Scanner sc = new Scanner(new FileReader("demo.txt"));
        int N = sc.nextInt();
        union_find uf = new union_find(N);
        while (sc.hasNext()) {
            int p = sc.nextInt();
            int q = sc.nextInt();
            if (uf.connected(p, q)) continue;
            uf.union(p, q);
            System.out.println(p + " " + q);
        }
        sc.close();
    }
}

# 小白尝试，代码简陋，不做参考
# 会改的会改的

class quick_union:
    def __init__(self, N):
        self.id = list(range(N))
        self.sz = [1]*N

    def connected(self, p, q):
        return self.find(p) == self.find(q)

    def find(self, p):
        tmp = p
        while p != self.id[p]:
            p = self.id[p]
        while tmp != self.id[tmp]:
			t = tmp
			tmp = self.id[tmp]
			self.id[t] = p
        return p

    def union(self, p, q):
        pR = self.find(p)
        qR = self.find(q)
        # 若已经相连则不再创建连接
        if pR == qR:
            return
        if self.sz[pR] < self.sz[qR]:
            self.id[pR] = qR
            self.sz[qR] += self.sz[pR]
        else:
            self.id[qR] = pR
            self.sz[pR] += self.sz[qR]

f = open("demo.txt")
N = int(f.readline())
uf = quick_union(N)
fl = f.readlines()
f.close()
for s in fl:
    p = int(s.split(' ')[0])
    q = int(s.split(' ')[1])
    if uf.connected(p, q): continue
    uf.union(p, q)
    print("%d %d"%(p, q))

#include <iostream>
#include <fstream>
using namespace std;

class union_find {
private:
	int* id;
	int* sz;

public:
	union_find(int N) {
		id = new int[N];
		sz = new int[N];
		for (int i = 0; i < N; i++) {
			id[i] = i;
			sz[i] = 1;
		}
	}
	~union_find(){}

	bool connected(int p, int q) {
		return find(p) == find(q);
	}

	int find(int p) {
		int tmp = p;
		while (p != id[p]) p = id[p];
		while (tmp != id[tmp]) {
			int t = tmp;
			tmp = id[tmp];
			id[t] = p;
		}
		return p;
	}

    void Union(int p, int q) {
        // c++ 中 union 为共用体关键字
        int pR = find(p);
        int qR = find(q);
        if (pR == qR)
            return;
        if (sz[pR] < sz[qR]) {
            id[pR] = qR;
            sz[qR] += sz[pR];
        } else {
            id[qR] = pR;
            sz[pR] += sz[qR];
        }
    }
};

int main() {
	ifstream fin;
	fin.open("demo.txt");
	int N;
	fin >> N;
	union_find* uf = new union_find(N);

	int p, q;
	while (fin >> p) {
		fin >> q;
		if (uf->connected(p, q)) continue;
		uf->Union(p, q);
		cout << p << " " << q << endl;
	}
	fin.close();
}

参考文献

[1]Robert Sedgewick,Kevin Wayne.算法:第4版[M].谢路云,译.北京:人民邮电出版社,2012:136-149.
[2]中国国家标准化管理委员会.信息与文献参考文献著录规则:GB/T 7714—2015[S].北京:中华人民共和国国家质量监督检验检疫总局,2015.
[3]Bruce Eckel.Java编程思想:第4版[M].陈昊鹏,译.北京:机械工业出版社,2007.
[4]Stephen Prata.C++ Primer Plus（第6版）中文版[M].张海龙,袁国忠,译.北京:人民邮电出版社,2020.